Start Wykonaj potęgowanie jednostki urojonej:
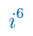
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Pochodne funkcji (122)
- Całki (215)
- Całki nieoznaczone (121)
- Całki oznaczone (32)
- Całki niewłaściwe (24)
- Całki podwójne (16)
- Całki potrójne (8)
- Całki krzywoliniowe (14)
- Funkcje (145)
- Szeregi i ciągi liczbowe (115)
- Ciągi liczbowe (20)
- Granice ciągów (38)
- Szeregi liczbowe (36)
- Szeregi potęgowe i funkcyjne (17)
- Szeregi Fouriera (4)
- Równania różniczkowe (44)
- Macierze i wyznaczniki (90)
- Działania na macierzach (22)
- Wyznacznik macierzy (24)
- Macierz odwrotna (16)
- Równania macierzowe (14)
- Rząd macierzy (10)
- Wartości i wektory własne (4)
- Liczby zespolone (134)
- Wielomiany (37)
- Równania i nierówności (3)
- Układy równań liniowych (29)
- Geometria analityczna (34)
- Logika (44)
- Zdania logiczne (22)
- Działania na zbiorach (22)
- Rachunek prawdopodobieństwa (84)
- Kombinatoryka (36)
- Prawdopodobieństwo (38)
- Zmienna losowa (6)
- Funkcja charakterystyczna (4)
- Statystyka matematyczna (5)
- Finanse (6)
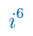
Wykonaj potęgowanie jednostki urojonej:
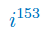
Wykonaj potęgowanie jednostki urojonej:
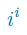
Wykonaj dzielenie liczb zespolonych:
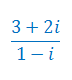
Wykonaj działania na liczbach zespolonych:
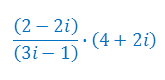
Wykonaj działania na liczbach zespolonych:
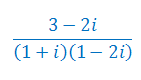
Wykonaj działania na liczbach zespolonych:
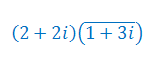
Wykonaj dzielenie liczb zespolonych:
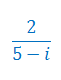
Wykonaj działania na liczbach zespolonych:
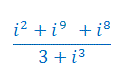
Wykonaj dzielenie liczb zespolonych:
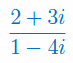
Podaj część rzeczywistą i urojoną liczby zespolonej:
\(z=\frac{1}{1-i}\)
Podaj część rzeczywistą i urojoną liczby zespolonej:
\(z=\frac{1+i}{1-i}\)
Podaj część rzeczywistą i urojoną liczby zespolonej:
\(z=\frac{1-i}{1+i}\)
Niech \(z=x+yi\), \(x,y\in\mathbb{R}\). Wyznacz część rzeczywistą i urojoną liczby zespolonej:
\(z^2\)
Niech \(z=x+yi\), \(x,y\in\mathbb{R}\). Jaka jest część rzeczywista i urojona liczby zespolonej:
\(z^3\)
Niech \(z=x+yi\), \(x,y\in\mathbb{R}\). Wyznacz część rzeczywistą i urojoną liczby zespolonej:
\(\frac{1}{z+i}\)
Wykonaj dzielenie liczb zespolonych:
\(\frac{(1+i)^2-2i^3}{(1-i)(1+i)}\)
Oblicz
\(\frac{1}{1-i}+\frac{1}{1+i}\)
Oblicz
\(\frac{1}{1-i}-\frac{1}{1+i}\)
Oblicz
\(\frac{1}{z}-\frac{1}{\overline{z}}\)
gdzie \(z\) jest liczbą zespoloną.
Oblicz
\(\frac{1}{z}+\frac{1}{\overline{z}}\)
gdzie \(z\) jest liczbą zespoloną.
Korzystając ze wzoru de Moivre'a oblicz potęgę:
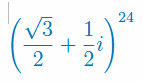
Korzystając ze wzoru de Moivre'a oblicz potęgę:
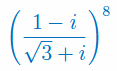
Podaj sprzężenie liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej
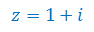
Oblicz moduł i argument liczby zespolonej:
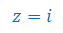
Oblicz moduł i sprzężenie liczby zespolonej:
\(z=1\)
Oblicz sprzężenie i moduł liczby zespolonej z:
\(z=-2i\)
Oblicz sprzężenie i moduł liczby zespolonej:
\(-3+4i\)
Wykaż, że:
\(z\cdot \overline{z}=|z|^2\)
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
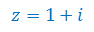
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
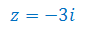
Oblicz moduł liczby zespolonej:
\(\left|\frac{\frac{\sqrt{3}}{2}+\frac{1}{2}i}{\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i}\right|\)
Oblicz moduł liczby zespolonej:
\(\big|(1+i)^{10}\cdot i^{2017}\big|\)
Wykaż, że:
\(|z_1\cdot z_2|=|z_1|\cdot |z_2|\)
Wykaż, że dla każdego \(n\in \mathbb{N}\):
\(|z^n|=|z|^n\)
Oblicz moduł i argument liczby zespolonej oraz zaznacz je na płaszczyźnie zespolonej:
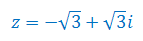
Oblicz moduł i argument liczby zespolonej:
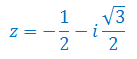
Oblicz moduł i argument liczby zespolonej:
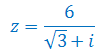
Oblicz moduł liczby zespolonej:
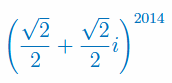
Niech \(z\neq 0\), będzie pewną liczbą zespoloną. Która z liczb ma najmniejszy moduł:
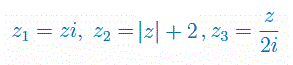
Udowodnij, że każda liczba zespolona \(z\neq -1\) o module równym 1 może być przedstawiona w postaci:
\(z=\frac{1+ti}{1-ti},\,\,\textrm{gdzie}\,\,t\in\mathbb{R}\)
Wykaż, że moduł liczby zespolonej \(z=\sin \alpha +\cos \alpha\, i\), \(\alpha\in\mathbb{R}\) jest równy 1.
Niech \(\arg(z)=\frac{\pi}{4}\). Wyznacz argument główny liczb zespolonych:
\((a)\, z^2\)
\((b)\, z^3\)
\((c)\, z^{100}\)
Wyznacz argumenty liczb zespolonych:
(a) \(\frac{\sqrt{3}}{2}+\frac{1}{2}i\)
(b) \(\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
(c) \(-\frac{1}{2}+\frac{\sqrt{3}}{2}i\)
(d) \(-\frac{\sqrt{3}}{2}+\frac{1}{2}i\)
(e) \(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
(f) \(\frac{1}{2}-\frac{\sqrt{3}}{2}i\)
Niech \(|z|=2\). Wyznacz moduły liczb zespolonych:
\((a)\, z^2\)
\((b)\, \frac{z^3}{2}\)
Rozwiąż nierówność z argumentem liczby zespolonej i wykonaj rysunek na płaszczyźnie zespolonej:
\(0< \arg(z)< \frac{\pi}{4}\)
Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych:
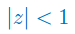
Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych:
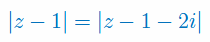
Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych:
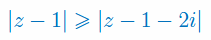
Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych:
\(\left|\frac{z-1}{z-1-2i}\right|=1\)
Na tej stronie znajdziesz około tysiąca zadań z rozwiązaniami i przykładów krok po kroku głównie z zakresu matematyki wyższej, jak również z matematyki na poziomie liceum. Zadania podzielone są na działy tematyczne zazwyczaj według przedmiotów i tematów wymaganych na studiach, np. zadania z pochodnych funkcji i całek (analiza matematyczna), macierzy i liczb zespolonych (algebra liniowa), zmiennych losowych i prawdopodobieństwa (rachunek prawdopodobieństwa) itd.
W każdej kategorii znajdziesz zadania o różnym poziomie trudności, a pod każdym zadaniem znajdziesz wiele wskazówek jak przebiega rozwiązanie, potrzebne definicje i wzory oraz podsumowanie schematów użytych w rozwiązaniu. Często rozwiązanie zadania omówione jest wręcz krok po kroku. Warto starać się samodzielnie rozwiązać jak najwięcej zadań znajdujących się na stronie, ponieważ są tu zebrane typowe zadania z kolokwiów i egzaminów z polskich uczelni. Nauka matematyki na przykładach i konkretnych zadaniach jest najbardziej efektywna - potwierdzają to badania naukowe. Trzeba tylko uczyć się (a właściwie analizować przykłady i rozwiązywać zadania) konsekwentnie i wytrwale, a efekty w postaci lepszego zrozumienia pojęć i schematów oraz umiejętność samodzielnego rozweiązywania podobnych zadań przyjdą same.
Pamiętaj, że zawsze masz możliwość zadania pytania w komentarzu pod każdym zadaniem - warto z tej możliwości korzystać, ponieważ na tej stronie nie ma głupich pytań i każde, nawet najgłupsze pytanie znajdzie swoją odpowiedź. Powodzenia w zrozumieniu matematyki!