Start Rozwiąż równanie zespolone:
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Pochodne funkcji (122)
- Całki (215)
- Całki nieoznaczone (121)
- Całki oznaczone (32)
- Całki niewłaściwe (24)
- Całki podwójne (16)
- Całki potrójne (8)
- Całki krzywoliniowe (14)
- Funkcje (145)
- Szeregi i ciągi liczbowe (115)
- Ciągi liczbowe (20)
- Granice ciągów (38)
- Szeregi liczbowe (36)
- Szeregi potęgowe i funkcyjne (17)
- Szeregi Fouriera (4)
- Równania różniczkowe (44)
- Macierze i wyznaczniki (90)
- Działania na macierzach (22)
- Wyznacznik macierzy (24)
- Macierz odwrotna (16)
- Równania macierzowe (14)
- Rząd macierzy (10)
- Wartości i wektory własne (4)
- Liczby zespolone (134)
- Wielomiany (37)
- Równania i nierówności (3)
- Układy równań liniowych (29)
- Geometria analityczna (34)
- Logika (44)
- Zdania logiczne (22)
- Działania na zbiorach (22)
- Rachunek prawdopodobieństwa (84)
- Kombinatoryka (36)
- Prawdopodobieństwo (38)
- Zmienna losowa (6)
- Funkcja charakterystyczna (4)
- Statystyka matematyczna (5)
- Finanse (6)
Rozwiąż równanie zespolone wiedząc, że \(Im(z)=1\):
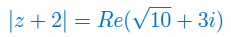
Rozwiąż równanie zespolone:
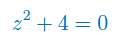
Rozwiąż równanie zespolone:
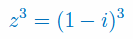
Rozwiąż równanie zespolone:
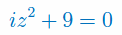
Rozwiąż równanie zespolone:
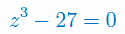
Rozwiąż równanie zespolone:
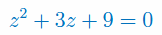
Rozwiąż równanie zespolone:
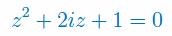
Znajdź wszystkie liczby zespolone spełniające równanie:
\((z+1)^n-(z-1)^n=0\)
gdzie \(n\in\mathbb{N}\).
Znajdź wszystkie wartości rzeczywiste parametru t, dla których spełnione są warunki
\(z^2=t+8i,\,\,\,\,\,\,\arg(z^2)=\frac{3}{4}\pi\)
Rozwiąż równanie zespolone:
\(1^x=-1\)
Rozwiąż równanie zespolone:
\(z^4=1\)
Rozwiąż równanie zespolone:
\(z^3=1\)
Rozwiąż równanie zespolone:
\(z^2=\overline{z}\)
Rozwiąż równanie zespolone:
\(z^3=\overline{z}\)
Wyznacz wszystkie pierwiastki wielomianu
\(W(x)=(x^2-1)(x-2)\)
Oblicz pierwiastki rzeczywiste wielomianu 3-go stopnia
\(W(x)=x^3-1\)
Znajdź wszystkie pierwiastki całkowite wielomianu
\(W(x)=x^3-2x^2-5x+6\)
Znajdź wszystkie pierwiastki wymierne wielomianu
\(W(x)=4x^4-7x^2-5x-1\)
Sprawdź, czy liczby 1 i 2 są pierwiastkami wielomianu
\(W(x)=x^3-2x^2-5x+6\)
Wyznacz pierwiastki wielomianu
\(W(x)=x^2+3x+9\)
Wyznacz wszystkie pierwiastki wielomianu
\(W(x)=x^3-3x^2+2\)
Oblicz pierwiastki zespolone wielomianu:
\({W(z)=z^2-i}\)
Oblicz pierwiastki zespolone wielomianu:
\(W(z)=z^4-1\)
Oblicz pierwiastki zespolone wielomianu:
\(W(z)=z^3-1\)
Obliczyć pierwiastki zespolone wielomianu:
\(W(z)=z^2+4\)
Oblicz pierwiastki zespolone wielomianu:
\(W(z)=z^2+2iz+1\)
Oblicz pierwiastki zespolone wielomianu:
\(W(z)=z^2+3z+9\)
Oblicz pierwiastki wielomianu:
\(W(z)=z^3-27\)
Oblicz pierwiastki wielomianu:
\(W(z)=iz^2+9\)
Wykonaj dodawanie wielomianów \(W(x)+Q(x)\), gdzie:
\(W(x)=2x^2+x-3\)
\(Q(x)=-x^3-5x+1\)
Oblicz iloczyn wielomianów rzeczywistych:
\(W(x)=x^2-2x-3\)
\(Q(x)=-x^3-5x^2+2x+1\)
Wykonaj dzielenie wielomianów \(W(x):Q(x)\) i podaj resztę:
\(W(x)=x^3+5x^2+7\)
\(Q(x)=x^2+1\)
Wykonaj odejmowanie wielomianów \(W(x)-Q(x)\), gdzie:
\(W(x)=-x^6-3x^2+2x-5\)
\(Q(x)=x^4-5x^2-4x+2\)
Określ stopień wielomianu i podaj wartość wyrazu wolnego:
\(W(x)=23x^5-x^4+3x+1\)
Oblicz iloczyn wielomianów zespolonych:
\(W(z)=z^2+3iz+2-i\)
\(Q(z)=-iz^2-4z+i\)
Określ stopień wielomianu \((W(x)+Q(x))\cdot P(x)\), gdzie:
\(W(x)=7x^3-1\)
\(Q(x)=2x^2+x\)
\(P(x)=-5x+3\)
Dla jakich wartości parametrów \(a\) i \(b\) stopnie wielomianów \(W(x)\) i \(Q(x)\) są równe:
\(W(x)=(a-2b)x^4+2ax^3-bx^2+1\)
\(Q(x)=(a+b)x^3-4ax+4\)
Oblicz iloraz oraz resztę z dzielenia wielomianu \(W(x)\) przez wielomian \(Q(x)\), gdzie:
\(W(z)=z^5+3z^2+7iz-1\)
\(Q(z)=z-i\)
Nie wykonując dzielenia wyznacz resztę z dzielenia wielomianu \(W(x)\) przez \(Q(x)\), gdzie:
\(W(x)=x^5+2x^4+3x+1\)
\(Q(x)=x^2+x-2\)
Rozłóż funkcję wymierną na ułamki proste
\(\frac{1}{(x-1)(x-2)}\)
Rozłożyć funkcję wymierną na ułamki proste
\(\frac{1}{x^2+4x-5}\)
Wyznaczyć rozkład funkcji na ułamki proste
\(\frac{-3x^2+4}{x(x+2)(x+3)}\)
Podaj rozkład funkcji na zespolone ułamki proste
\(\frac{1}{x^2+3x+9}\)
Podaj rozkład funkcji na rzeczywiste i zespolone ułamki proste
\(\frac{x^2-6x+1}{(x-3)^3}\)
Podaj rozkład funkcji na rzeczywiste i zespolone ułamki proste
\(\frac{x}{x^2+1}\)
Określ, które funkcje wymierne są rzeczywistymi ułamkami prostymi:
(a) \(\frac{1}{x-1}\)
(b) \(\frac{2x+3}{x^2+2x+1}\)
(c) \(\frac{-x}{4x^2+x+2}\)
Określ, które funkcje wymierne są zespolonymi ułamkami prostymi:
(a) \(\frac{ix}{(x-i)^2}\)
(b) \(\frac{2i}{x-2+3i}\)
(c) \(\frac{1}{4x^2+4}\)
Podaj rozkład funkcji wymiernej na zespolone ułamki proste
\(\frac{x^4-x^3+2}{x(x-1)^3(x^2+1)}\)
Podaj rozkład funkcji wymiernej na rzeczywiste ułamki proste
\(\frac{x^4-x^3+2}{x(x-1)^3(x^2+1)}\)
Na tej stronie znajdziesz około tysiąca zadań z rozwiązaniami i przykładów krok po kroku głównie z zakresu matematyki wyższej, jak również z matematyki na poziomie liceum. Zadania podzielone są na działy tematyczne zazwyczaj według przedmiotów i tematów wymaganych na studiach, np. zadania z pochodnych funkcji i całek (analiza matematyczna), macierzy i liczb zespolonych (algebra liniowa), zmiennych losowych i prawdopodobieństwa (rachunek prawdopodobieństwa) itd.
W każdej kategorii znajdziesz zadania o różnym poziomie trudności, a pod każdym zadaniem znajdziesz wiele wskazówek jak przebiega rozwiązanie, potrzebne definicje i wzory oraz podsumowanie schematów użytych w rozwiązaniu. Często rozwiązanie zadania omówione jest wręcz krok po kroku. Warto starać się samodzielnie rozwiązać jak najwięcej zadań znajdujących się na stronie, ponieważ są tu zebrane typowe zadania z kolokwiów i egzaminów z polskich uczelni. Nauka matematyki na przykładach i konkretnych zadaniach jest najbardziej efektywna - potwierdzają to badania naukowe. Trzeba tylko uczyć się (a właściwie analizować przykłady i rozwiązywać zadania) konsekwentnie i wytrwale, a efekty w postaci lepszego zrozumienia pojęć i schematów oraz umiejętność samodzielnego rozweiązywania podobnych zadań przyjdą same.
Pamiętaj, że zawsze masz możliwość zadania pytania w komentarzu pod każdym zadaniem - warto z tej możliwości korzystać, ponieważ na tej stronie nie ma głupich pytań i każde, nawet najgłupsze pytanie znajdzie swoją odpowiedź. Powodzenia w zrozumieniu matematyki!