Oblicz całkę z funkcji dwóch zmiennych:
\((a)\,\,\int x\cos y\,dx\)
\((b)\,\,\int x\cos y\,dy\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Oblicz całkę z funkcji dwóch zmiennych:
\((a)\,\,\int x\cos y\,dx\)
\((b)\,\,\int x\cos y\,dy\)
Oblicz całkę podwójną
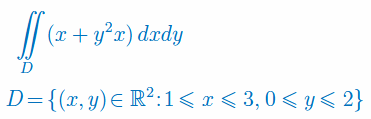
Oblicz całkę podwójną
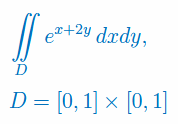
Oblicz całkę podwójną
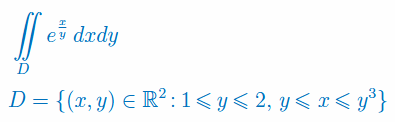
Oblicz całkę podwójną
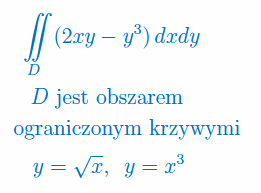
Oblicz całkę podwójną
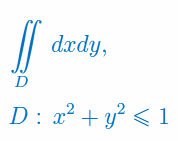
Oblicz całkę podwójną
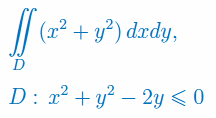
Oblicz całkę podwójną
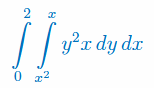
Oblicz całkę podwójną
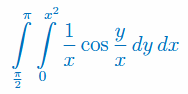
Oblicz całkę podwójną
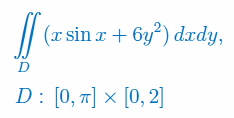
Oblicz całkę podwójną
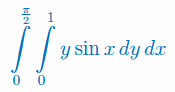
Oblicz całkę podwójną
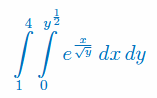
Oblicz całkę podwójną
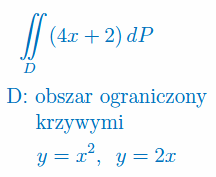
Oblicz całkę podwójną
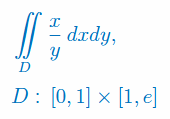
Oblicz całkę podwójną
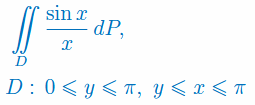
Oblicz całkę potrójną
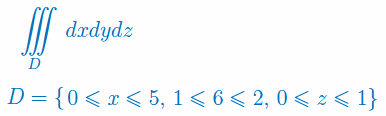
Oblicz całkę potrójną
\(\iiint \limits_D x\cdot y\,dxdydz,\,\,D=\left\{0\le x\le 1,\,0\le y\le 1,\,\,0\le z\le 1\right\}\)
Oblicz całkę potrójną
\(\iiint \limits_D x\cdot (y+z)\,dxdydz,\,\,D=\left\{0\le x\le 1,\,0\le y\le 1,\,\,0\le z\le 1\right\}\)
Oblicz całkę potrójną
\(\iiint \limits_D x\sin(y+z)\,dxdydz,\,\,D=\left\{0\le x\le 1,\,0\le y\le \frac{\pi}{4},\,\,0\le z\le \frac{\pi}{4}\right\}\)
Oblicz całkę potrójną
\(\iiint \limits_D x\cdot y\cdot z\,dxdydz,\,\,D=\left\{0\le x\le 1,\,0\le y\le 1,\,\,0\le z\le 1\right\}\)
Oblicz całkę potrójną
\(\iiint \limits_D (x+y+z)\,dxdydz,\,\,D=\left\{0\le x\le 1,\,0\le y\le 1,\,\,0\le z\le 1\right\}\)
Oblicz całkę potrójną
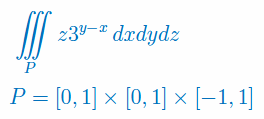
Oblicz całkę potrójną
\(\iiint \limits_D x\cdot z\,dxdydz,\,\,D=\left\{0\le x\le 1,\,0\le y\le 1,\,\,0\le z\le e^y\right\}\)
Oblicz całkę krzywoliniową skierowaną daną równaniem funkcyjnym
\(\int\limits_L 2xy\, dx+ x^2 \,dy\)
gdzie L jest łukiem paraboli \(y(x)=x^2\) dla \(x\in[0,1]\).
Oblicz całkę krzywoliniową
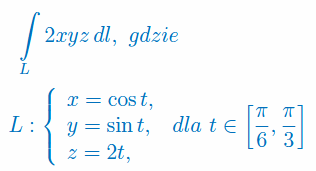
Oblicz całkę krzywoliniową
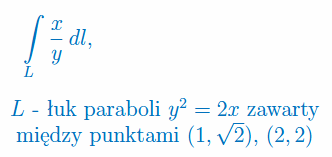
Oblicz długość łuku
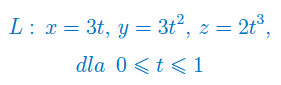
Obliczyć długość łuku linii zadanej w postaci parametrycznej
\(x=3 \cos t,\,y=3\sin t,\,z=4t\) dla \(t\in[0,1]\).
Obliczyć masę jednorodnego półokręgu
\(L:x^2+y^2=R^2,\,\,y\ge 0,\,\,\rho=C=const\).
Obliczyć momenty statyczne jednorodnego półokręgu
\(L:x^2+y^2=R^2,\,\,y\ge 0,\,\,\rho=C=const\).
Obliczyć współrzędne środka masy jednorodnego półokręgu
\(L:x^2+y^2=R^2,\,\,y\ge 0,\,\,\rho=C=const\).
Oblicz całkę krzywoliniową skierowaną daną równaniem funkcyjnym
\(\int\limits_L xy\, dx-x^2 \,dy\)
gdzie L jest łukiem zadanym równaniem \(y(x)=\frac{1}{x}\) dla \(x\in[1,4]\).
Oblicz całkę krzywoliniową skierowaną daną równaniem funkcyjnym
\(\int\limits_L \frac{y}{x}\, dx+ \frac{x}{y} \,dy\)
gdzie L jest łukiem paraboli \(y(x)=x^2\) dla \(x\in[-1,1]\).
Oblicz całkę krzywoliniową skierowaną
\(\int\limits_L dx+\,dy+\,dz\)
gdzie L jest łukiem zadanym równaniem parametrycznym \(x=t,\,y=t,\,z=t\) dla \(t\in[0,1]\).
Oblicz całkę krzywoliniową skierowaną
\(\int\limits_L x\, dx+y \,dy+z\,dz\)
gdzie L jest łukiem zadanym równaniem parametrycznym \(x=2t,\,y=t^2,\,z=1-t\) dla \(t\in[0,1]\).
Obliczyć długość łuku linii zadanej w postaci parametrycznej
\(x=t,\,y= t,\,z=t\) dla \(t\in[0,1]\).
Oblicz całkę krzywoliniową skierowaną
\(\int\limits_L y\, dx+2x \,dy\)
gdzie L jest łukiem zadanym równaniem parametrycznym \(x=t-\sin t,\,y=1-\cos t\) dla \(t\in[0,2\pi]\).
Wyznacz dziedzinę i narysuj wykres funkcji

Określ dziedzinę funkcji (dla \(x\in\mathbb{R}\))
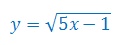
Określ dziedzinę funkcji
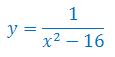
Określ dziedzinę funkcji
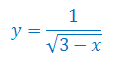
Wyznacz dziedzinę, miejsca zerowe i zbiór wartości funkcji wymiernej
\(f(x)=\frac{2}{x+3}+4\)
Oblicz miejsca zerowe funkcji
\(f(x)=\frac{(x-1)(x+2)}{\sqrt{x}-1}\)
Podaj przykład funkcji, której dziedziną jest zbiór liczb rzeczywistych dodatnich.
Podaj przykład funkcji wymiernej, która dla argumentu równego 1 przyjmuje wartość 5, a jej dziedziną jest zbiór:
\(D_f=\mathbb{R}\setminus \{0\}\)
Wyznacz dziedzinę funkcji
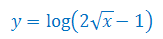
Wyznacz dziedzinę funkcji
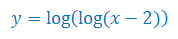
Wyznacz dziedzinę funkcji
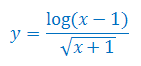
Wyznacz dziedzinę funkcji
\((a)\,\, f(x)=\ln(|x|+1)\)
\((b)\,\, f(x)=\ln(|x|-1)\)
Wyznacz dziedzinę funkcji
Na tej stronie znajdziesz około tysiąca zadań z rozwiązaniami i przykładów krok po kroku głównie z zakresu matematyki wyższej, jak również z matematyki na poziomie liceum. Zadania podzielone są na działy tematyczne zazwyczaj według przedmiotów i tematów wymaganych na studiach, np. zadania z pochodnych funkcji i całek (analiza matematyczna), macierzy i liczb zespolonych (algebra liniowa), zmiennych losowych i prawdopodobieństwa (rachunek prawdopodobieństwa) itd.
W każdej kategorii znajdziesz zadania o różnym poziomie trudności, a pod każdym zadaniem znajdziesz wiele wskazówek jak przebiega rozwiązanie, potrzebne definicje i wzory oraz podsumowanie schematów użytych w rozwiązaniu. Często rozwiązanie zadania omówione jest wręcz krok po kroku. Warto starać się samodzielnie rozwiązać jak najwięcej zadań znajdujących się na stronie, ponieważ są tu zebrane typowe zadania z kolokwiów i egzaminów z polskich uczelni. Nauka matematyki na przykładach i konkretnych zadaniach jest najbardziej efektywna - potwierdzają to badania naukowe. Trzeba tylko uczyć się (a właściwie analizować przykłady i rozwiązywać zadania) konsekwentnie i wytrwale, a efekty w postaci lepszego zrozumienia pojęć i schematów oraz umiejętność samodzielnego rozweiązywania podobnych zadań przyjdą same.
Pamiętaj, że zawsze masz możliwość zadania pytania w komentarzu pod każdym zadaniem - warto z tej możliwości korzystać, ponieważ na tej stronie nie ma głupich pytań i każde, nawet najgłupsze pytanie znajdzie swoją odpowiedź. Powodzenia w zrozumieniu matematyki!