Oblicz pochodną funkcji złożonej
\(y=4\arccos^8(x)\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Oblicz pochodną funkcji złożonej
\(y=4\arccos^8(x)\)
Oblicz pochodną funkcji
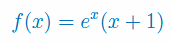
Oblicz pochodną funkcji złożonej
\(y={(\sin(x))}^{\cos(x)}\)
Oblicz pochodną funkcji
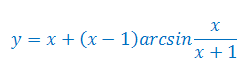
Oblicz pochodną funkcji
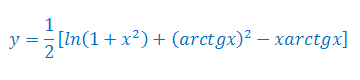
Oblicz pochodną funkcji
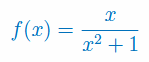
Oblicz pochodną funkcji
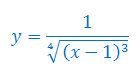
Oblicz pochodną funkcji
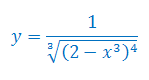
Oblicz pochodną funkcji
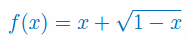
Oblicz pochodną funkcji
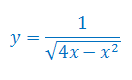
Oblicz pochodną funkcji złożonej
\(y=(f(x))^{g(x)}\)
Oblicz pochodną funkcji
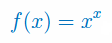
Oblicz pochodną funkcji
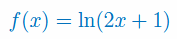
Oblicz pochodną funkcji
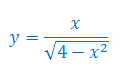
Oblicz pochodną funkcji
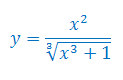
Oblicz pochodną funkcji
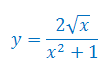
Oblicz pochodną funkcji
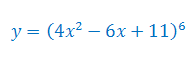
Oblicz pochodną funkcji
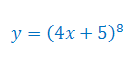
Oblicz pochodną funkcji
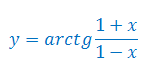
Oblicz pochodną funkcji
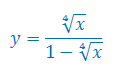
Oblicz pochodną funkcji
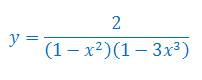
Oblicz pochodną funkcji
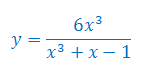
Oblicz pochodną funkcji
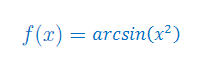
Oblicz pochodną funkcji
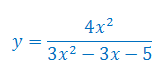
Oblicz pochodną funkcji
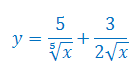
Oblicz pochodną funkcji
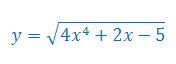
Oblicz pochodną funkcji
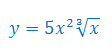
Oblicz pochodną funkcji
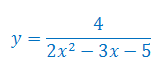
Oblicz pochodną funkcji
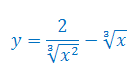
Oblicz pochodną funkcji
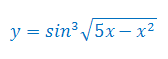
Oblicz pochodną funkcji
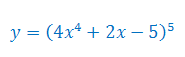
Oblicz pochodną funkcji
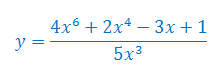
Oblicz pochodną funkcji
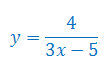
Oblicz pochodną funkcji
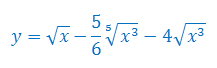
Oblicz pochodną funkcji
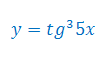
Oblicz pochodną funkcji
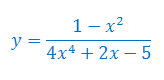
Oblicz pochodną funkcji
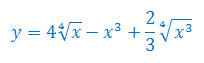
Oblicz pochodną funkcji
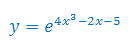
Oblicz pochodną funkcji
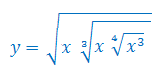
Oblicz pochodną funkcji
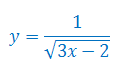
Oblicz pochodną funkcji
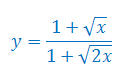
Oblicz pochodną funkcji
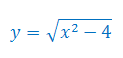
Oblicz pochodną funkcji
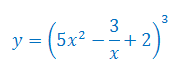
Oblicz pochodną funkcji
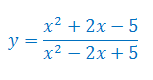
Oblicz pochodną funkcji
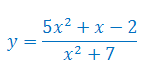
Oblicz pochodną funkcji
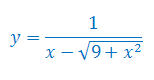
Oblicz pochodną funkcji
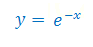
Oblicz pochodną funkcji
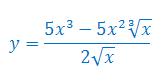
Oblicz pochodną funkcji
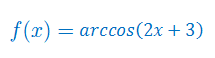
Oblicz pochodną funkcji
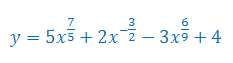
Na tej stronie znajdziesz około tysiąca zadań z rozwiązaniami i przykładów krok po kroku głównie z zakresu matematyki wyższej, jak również z matematyki na poziomie liceum. Zadania podzielone są na działy tematyczne zazwyczaj według przedmiotów i tematów wymaganych na studiach, np. zadania z pochodnych funkcji i całek (analiza matematyczna), macierzy i liczb zespolonych (algebra liniowa), zmiennych losowych i prawdopodobieństwa (rachunek prawdopodobieństwa) itd.
W każdej kategorii znajdziesz zadania o różnym poziomie trudności, a pod każdym zadaniem znajdziesz wiele wskazówek jak przebiega rozwiązanie, potrzebne definicje i wzory oraz podsumowanie schematów użytych w rozwiązaniu. Często rozwiązanie zadania omówione jest wręcz krok po kroku. Warto starać się samodzielnie rozwiązać jak najwięcej zadań znajdujących się na stronie, ponieważ są tu zebrane typowe zadania z kolokwiów i egzaminów z polskich uczelni. Nauka matematyki na przykładach i konkretnych zadaniach jest najbardziej efektywna - potwierdzają to badania naukowe. Trzeba tylko uczyć się (a właściwie analizować przykłady i rozwiązywać zadania) konsekwentnie i wytrwale, a efekty w postaci lepszego zrozumienia pojęć i schematów oraz umiejętność samodzielnego rozweiązywania podobnych zadań przyjdą same.
Pamiętaj, że zawsze masz możliwość zadania pytania w komentarzu pod każdym zadaniem - warto z tej możliwości korzystać, ponieważ na tej stronie nie ma głupich pytań i każde, nawet najgłupsze pytanie znajdzie swoją odpowiedź. Powodzenia w zrozumieniu matematyki!