Na podstawie kilku początkowych wyrazów ciągu znaleźć jego wzór ogólny:
\((a_n)=(2,4,8,16,...)\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Na podstawie kilku początkowych wyrazów ciągu znaleźć jego wzór ogólny:
\((a_n)=(2,4,8,16,...)\)
Na podstawie kilku początkowych wyrazów ciągu znajdź jego wzór ogólny:
\((a_n)=(6,4,2,0,-2,...)\)
Na podstawie kilku początkowych wyrazów ciągu znaleźć jego wzór ogólny:
\((a_n)=\left(-1,-\frac{1}{3},-\frac{1}{9},-\frac{1}{27},...\right)\)
Na podstawie kilku początkowych wyrazów ciągu znaleźć jego wzór ogólny:
\((a_n)=(-1,2,5,8,11,...)\)
Podaj przykład ciągu rosnącego o wyrazach:
(a) dodatnich
(b) ujemnych
Podaj przykład ciągu malejącego o wyrazach:
(a) ujemnych
(b) dodatnich
Zbadaj monotoniczność ciągu liczbowego:
\(a_n=n+1\)
Zbadać monotoniczność ciągu liczbowego:
\(a_n=(-1)^{2n}\)
Zbadaj monotoniczność ciągu liczbowego:
\(a_n=\frac{n}{2n+1}\)
Zbadaj monotoniczność ciągu liczbowego:
\(a_n=\frac{1}{n}\)
Podaj wzór ogólny ciągu:
\((a_n)=\left(1,4,9,16,...\right)\)
Podaj wzór ogólny ciągu:
\((a_n)=\left(1,4,27,16,256,...\right)\)
Podaj wzór ogólny ciągu:
\((a_n)=\left(1,2,6,24,120,720,...\right)\)
Podaj wzór ogólny ciągu:
\((a_n)=\left(-1,4,-9,16,...\right)\)
Wykaż, że ciąg \(a_n\) jest rosnący
\(a_n=\frac{3n+1}{n+2}\)
Podaj przykład ciągu malejącego o wyrazach:
(a) większych od 10
(b) mniejszych od -2
Wykaż, że ciąg \(a_n\) jest malejący
\(a_n=\frac{1}{n+1}\)
Podaj przykład ciągu rosnącego o wyrazach:
(a) większych od 7
(b) mniejszych od -5
Zbadać monotoniczność ciągu liczbowego:
\(a_n=(-1)^{n}\)
Zbadać monotoniczność ciągu:
\(a_n=\frac{7n-5}{3n-1}\)
Podaj wzór na granicę ciągu:
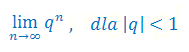
Oblicz granicę ciągu liczbowego:
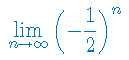
Oblicz granicę ciągu:
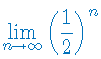
Podaj wzór na granicę:
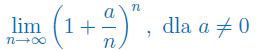
Oblicz granicę ciągu:
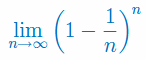
Oblicz granicę ciągu:
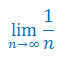
Obliczyć granicę ciągu liczbowego:
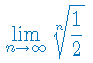
Oblicz granicę ciągu liczbowego:
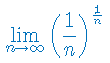
Oblicz granicę ciągu liczbowego:
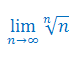
Podaj wzór na granicę ciągu liczbowego:
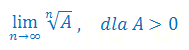
Podaj wzór na granicę:
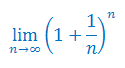
Wykaż, że granica ciągu nie istnieje:
\(\lim\limits_{n\to +\infty} (-1)^n\)
Oblicz granicę ciągu:
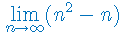
Obliczyć granicę ciągu liczbowego:
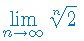
Wykaż, że dla \(a>0,\,\,b>0,\,c>0\) granica ciągu wynosi:
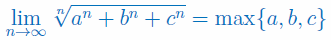
Wykaż, że dla \(a>0,\,\,b>0\) granica ciągu wynosi:
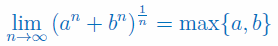
Oblicz granicę ciągu:
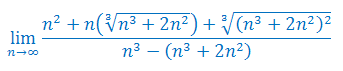
Oblicz granicę ciągu:
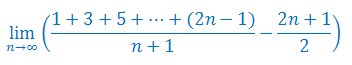
Oblicz granicę ciągu:
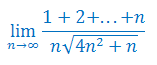
Oblicz granicę ciągu o wyrazie ogólnym \(a_n\), jeśli
\(a_n=\sqrt{2n}-\sqrt{n+10}\)
Oblicz granicę ciągu:
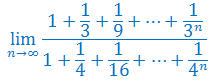
Oblicz granicę ciągu:
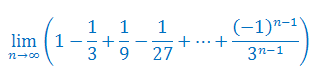
Oblicz granicę ciągu:
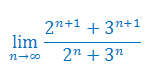
Oblicz granicę ciągu:
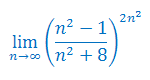
Oblicz granicę ciągu:
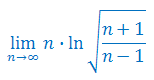
Oblicz granicę ciągu:
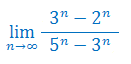
Oblicz granicę ciągu:
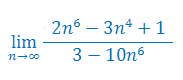
Oblicz granicę ciągu:
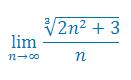
Oblicz granicę ciągu:
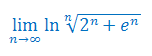
Oblicz granicę ciągu:
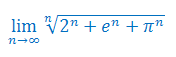
Jesteś w kategorii Ciągi i szeregi liczbowe zadania z rozwiązaniami
W tej kategorii znajdziesz rozwiązania typowych zadań dotyczących ciągów i szeregów liczbowych, w tym przykłady sprawdzania monotoniczności i ograniczonośći ciągów, liczenia granic ciągów, badania zbierzności szeregów liczbowych, funkcyjnych oraz szeregów Fouriera. Typowe schematy i pojęcia dotyczące granic ciągów to twierdzenie o dwóch i trzech ciągach, natomiast w przypadku szeregów liczbowych niezwykle ważne są kryteria zbieżnośći szeregów tj. kryterium porównawcze, ilorazowe, całkowe oraz kryterium d'Alemberta i Cauchy'ego. Szeregi funkcyjne związane są z kolei z pojęciem promienia zbieżnośći.
Po zapoznaniu się z możliwie dużą liczbą rozwiązań zadań z ciągów i szeregów liczbowych, warto spróbować samodzielnie rozwiązać ponownie te same lub podobne zadania, ale tym razem nie należy zaglądać do rozwiązań zamieszczonych na stronie (chyba, że jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku). Warto pamiętać, że pod każdym zadaniem masz sznasę zadać pytania w komentarzach. Zwróć uwagę, że tylko pełne zrozumienie rozwiązania zadania (oraz schematów i pojęć, które zostały w nim użyte) pozwala później na samodzielne rozwiązanie podobnego zadania w czasie trwania kolokwium lub egzaminu (tym bardziej w sytuacji stresującej).
Zadania z ciągów i szeregów są dość różnorodne i wymagają opanowania wielu schematów i metod (jak choćby kryteria zbieżnośći szeregów liczbowych), dlatego aby wyrobić sobie odpowidnią intuicję należy rozwiązać conajmniej kilkadziesiąt zadań i przykładów.