Start Wyznacz przedział zbieżności szeregu:
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Kategorie zadań z rozwiązaniami z matematyki wyższej
- Ciągi liczbowe (20)
- Granice ciągów (38)
- Szeregi liczbowe (36)
- Szeregi potęgowe i funkcyjne (17)
- Szeregi Fouriera (4)
Strona 3 z 3
Zadania z granic ciągów i szeregów liczbowych
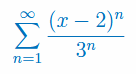
Wyznacz przedział zbieżności szeregu:
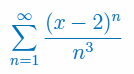
Wyznacz przedział zbieżności szeregu:
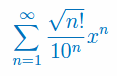
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
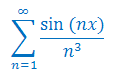
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
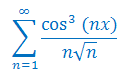
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego dla \(x\ge 0\):
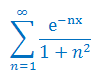
Korzystając z Tw. Weierstrassa uzasadnij zbieżność bezwzględną i jednostajną szeregu funkcyjnego:
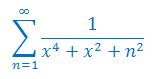
Zbadaj zbieżność jednostajną szeregu funkcyjnego:
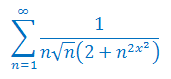
Zbadaj zbieżność jednostajną szeregu funkcyjnego:
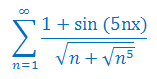
Zbadaj zbieżność jednostajną szeregu funkcyjnego:
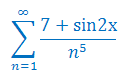
Zbadaj zbieżność jednostajną szeregu funkcyjnego dla \(x\ge 0\):
\(\sum\limits_{n=1}^\infty \frac{e^{-x}}{x+n^4}\)
Rozwiń w szereg Fouriera funkcję \(f(x)\) na przedziale \([-\pi,\pi]\):
\(f(x)=\left\{\begin{array}{cl}-1,&\textrm{dla}\,\,-\pi<x<0\\0,&\textrm{dla}\,\,x\in\{-\pi,0,\pi\}\\1,&\textrm{dla}\,\,0<x<\pi\end{array}\right.\)
Rozwiń w szereg Fouriera funkcję \(f(x)=|x|\) na przedziale \([-\pi,\pi]\).
Rozwiń w szereg Fouriera funkcję \(f(x)=x^2\) na przedziale \([-\pi,\pi]\).
Rozwiń w szereg Fouriera funkcję \(f(x)=x\) na przedziale \((-\pi,\pi)\).
Strona 3 z 3
Jesteś w kategorii Ciągi i szeregi liczbowe zadania z rozwiązaniami
W tej kategorii znajdziesz rozwiązania typowych zadań dotyczących ciągów i szeregów liczbowych, w tym przykłady sprawdzania monotoniczności i ograniczonośći ciągów, liczenia granic ciągów, badania zbierzności szeregów liczbowych, funkcyjnych oraz szeregów Fouriera. Typowe schematy i pojęcia dotyczące granic ciągów to twierdzenie o dwóch i trzech ciągach, natomiast w przypadku szeregów liczbowych niezwykle ważne są kryteria zbieżnośći szeregów tj. kryterium porównawcze, ilorazowe, całkowe oraz kryterium d'Alemberta i Cauchy'ego. Szeregi funkcyjne związane są z kolei z pojęciem promienia zbieżnośći.
Po zapoznaniu się z możliwie dużą liczbą rozwiązań zadań z ciągów i szeregów liczbowych, warto spróbować samodzielnie rozwiązać ponownie te same lub podobne zadania, ale tym razem nie należy zaglądać do rozwiązań zamieszczonych na stronie (chyba, że jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku). Warto pamiętać, że pod każdym zadaniem masz sznasę zadać pytania w komentarzach. Zwróć uwagę, że tylko pełne zrozumienie rozwiązania zadania (oraz schematów i pojęć, które zostały w nim użyte) pozwala później na samodzielne rozwiązanie podobnego zadania w czasie trwania kolokwium lub egzaminu (tym bardziej w sytuacji stresującej).
Zadania z ciągów i szeregów są dość różnorodne i wymagają opanowania wielu schematów i metod (jak choćby kryteria zbieżnośći szeregów liczbowych), dlatego aby wyrobić sobie odpowidnią intuicję należy rozwiązać conajmniej kilkadziesiąt zadań i przykładów.