Oblicz całkę oznaczoną
\[\int\limits_{1}^2 \left(\frac{2}{3x^2}+\frac{3}{2x}\right)\, dx\]
Rozwiązanie
Najpierw liczymy całkę nieoznaczoną:
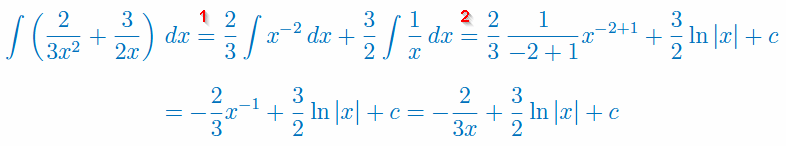
Teraz możemy obliczyć całkę oznaczoną:
\[\int\limits_{1}^2 \left(\frac{2}{3x^2}+\frac{3}{2x}\right)\, dx=\left[-\frac{2}{3x}+\frac{3}{2}\ln |x|\right]_{x=1}^{x=2}=\]
\[=-\frac{2}{6}+\frac{3}{2}\ln 2-\left(-\frac{2}{3}+\frac{3}{2}\ln 1\right)=-\frac{1}{3}+\frac{3}{2}\ln 2+\frac{2}{3}-0=\frac{1}{3}+\frac{3}{2}\ln 2\]
Wskazówki
- Korzystamy z własności całki nieoznaczonej (całka sumy funkcji jest sumą całek każdej funkcji z osobna, stałe a i b można wyjąć przed całkę)
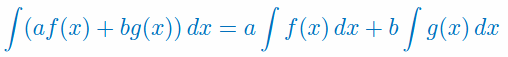
- Korzystamy z podstawowych wzorów na całki funkcji elementarnych:

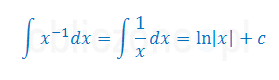
Sprawdzenie
\((-\frac{2}{3x}+\frac{3}{2}\ln|x|+c)'=-\frac{2}{3}\left(\frac{1}{x}\right)'+\frac{3}{2}(\ln|x|)'=\frac{2}{3x^2}+\frac{3}{2x}\)
Sprawdź wynik również za pomocą kalkulatora całek na stronie wolframalpha.com

Komentarzy (0)