Oblicz całkę nieoznaczoną
\[\int\limits_1^2 ln(x)\,dx\]
Rozwiązanie
Liczymy najpierw całkę nieoznaczoną - do obliczenia całki z lnx zastosujemy całkowanie przez części
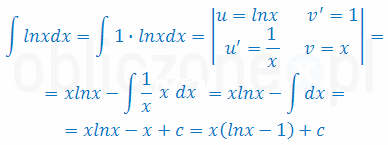
Teraz liczymy całkę oznaczoną:
\[\int\limits_{1}^2 ln(x)\,dx=[x\ln x-x]_{x=1}^{x=2}=2\ln 2-2-(1\cdot \ln 1-1)=2\ln 2-2-0+1=2\ln 2-1\]
Wskazówki
- \(\ln x=1\cdot \ln x \) słownie "jeden razy lnx".
Zawsze pamiętaj o dodatkowej "jedynce", która przydaje się często przy całkowaniu przez części! - Stosujemy całkowanie przez części.
- Korzystamy z faktu, że
\((x)'=1\) dlaego \(\int \,dx=\int 1 \,dx=x+c\)

Komentarzy (0)