Kolokwium - Zestaw 5
Zakres materiału: Pochodne funkcji
Rozwiązanie widoczne po rejestracji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Zakres materiału: Pochodne funkcji
Zadanie 1
Korzystając z definicji zbadaj czy istnieje pochodna funkcji w punkcie \(x_0=0\):
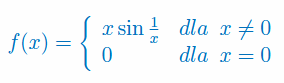
Zadanie 2
Oblicz pochodną funkcji
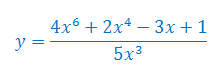
Zadanie 3
Napisz równanie stycznej do wykresu funkcji \(f(x)\) w punkcie \(x_0\)

Zadanie 4
Oblicz drugą pochodną funkcji:
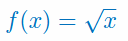
Rozwiązanie widoczne po rejestracji
Komentarzy (2)