NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
 Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!

Logowanie

Kolokwium - Zestaw 7

Zakres materiału: Układy równań liniowych

Kliknij i zobacz zadania

Zadanie 1

Rozwiąż układ równań z 3 niewiadomymi metodą macierzową:

Układ równań z parametrem, zadanie 2

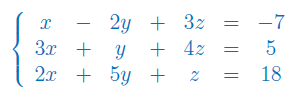
Zadanie 2

Rozwiąż układ Cramera z 3 niewiadomymi:

Wzory Cramera, zadanie 1

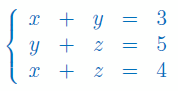
Zadanie 3

Rozwiązać układ równań metodą wyznacznikową:

Wzory Cramera, zadanie 4

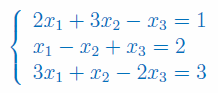
Zadanie 4

Zbadaj liczbę rozwiązań układu równań w zależności od parametru p. Dla p=2, korzystając ze wzorów Cramera wyznacz wartość niewiadomej y:

Układ równań z parametrem, zadanie 6

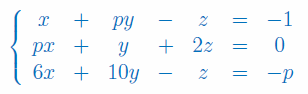
Rozwiązanie widoczne po rejestracji

Komentarzy (2)

  • Sebastian
    Sebastian 6 lat temu
    @Esemesika Dla \(p=3\) rząd macierzy głównej (\(rzA\) lub według Pani oznaczeń \(R(A)\)) i rozszerzonej (\(rz[A|B]\) - u Pani \(R(Au)\)) układu wynosi 2 (można to sprawdzić w kalkulatorze rzędu macierzy), dlatego zgodnie z Twierdzeniem Kroneckera-Capellego układ ma wtedy nieskończenie wiele rozwiązań. Proszę jeszcze raz policzyć rząd macierzy rozszerzonej \(R(Au)\) - powinien być równy 2 a nie 3.
  • Esemesika
    Esemesika 7 lat temu
    Dlaczego dla \(p=3\) jest nieskończenie wiele rozwiązań?... Robiłam innym sposobem wychodzi mi \(R(A)=2\) a \(R(Au)=3\) więc wychodzi brak rozwiązań.