Egzamin - Zestaw 1
Zakres materiału: Macierze, Liczby zespolone, Układy równań liniowych
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Zakres materiału: Macierze, Liczby zespolone, Układy równań liniowych
Zadanie 1
Znaleźć wartości x, które spełniają równanie z wyznacznikiem:
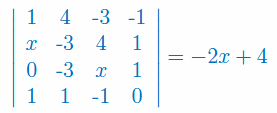
Zadanie 2
Niech \(z\neq 0\), będzie pewną liczbą zespoloną. Która z liczb ma najmniejszy moduł:
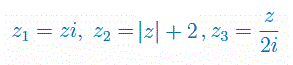
Zadanie 3
Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych:
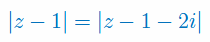
Zadanie 4
Rozwiązać układ równań metodą eliminacji Gaussa:
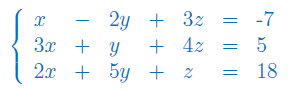
Zadanie 5
Określić liczbę rozwiązań układu równań przy użyciu twierdzenia Kroneckera-Capellego:
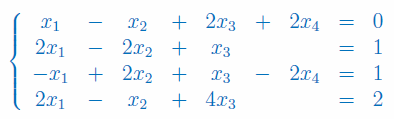
Zakres materiału: Macierze, Liczby zespolone, Układy równań liniowych
Zadanie 1
Oblicz wyznacznik macierzy 6x6:
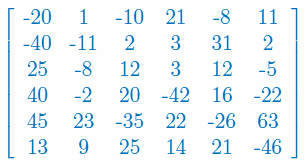
Zadanie 2
Oblicz moduł liczby zespolonej:
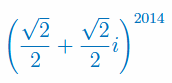
Zadanie 3
Narysuj na płaszczyźnie zespolonej zbiór liczb zespolonych:
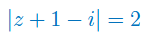
Zadanie 4
Stosując wzory Cramera wyznacz niewiadomą y
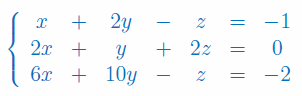
Zadanie 5
Rozwiązać układ równań przy użyciu metody eliminacji Gaussa:
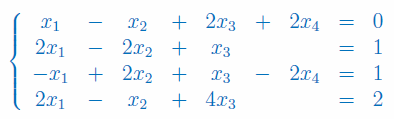
Zakres materiału: Macierze, Liczby zespolone, Wielomiany, Układy równań liniowych
Zadanie 1
Wykonaj działania na macierzach:
\(\left(\left[\begin{array}{cc}1&0\\1&2\end{array}\right]^T-\left[\begin{array}{cc}0&2\\-1& 0\end{array}\right]\right)\cdot \left[\begin{array}{ccc}1&0&-1\\-1& 2&0\end{array}\right]\)
Zadanie 2
Oblicz potęgę liczby zespolonej:
\((1+i)^8\)
Zadanie 3
Nie wykonując dzielenia wyznacz resztę z dzielenia wielomianu \(W(x)\) przez \(Q(x)\), gdzie:
\(W(x)=x^5+2x^4+3x+1\)
\(Q(x)=x^2+x-2\)
Zadanie 4
Oblicz pierwiastki zespolone wielomianu:
\(W(z)=z^2+2iz+1\)
Zadanie 5
Rozwiąż metodą eliminacji Gaussa:
\(\left\{\begin{array}{ccccccccc}2x_1&+&x_2&-&x_3&+&x_4&=&1\\&& x_2& +&3x_3&-&3x_4&=&1\\x_1&+&x_2&+&x_3&-&x_4&=&1\end{array}\right.\)
Zakres materiału: Macierze, Liczby zespolone, Wielomiany, Geometria analityczna, Układy równań liniowych
Zadanie 1
Rozwiąż układ równań z 3 niewiadomymi metodą macierzową:
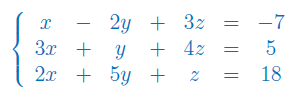
Zadanie 2
Rozwiąż nierówność z argumentem liczby zespolonej i wykonaj rysunek na płaszczyźnie zespolonej:
\(0< \arg(z)< \frac{\pi}{4}\)
Zadanie 3
Wyznaczyć rozkład funkcji na ułamki proste
\(\frac{-3x^2+4}{x(x+2)(x+3)}\)
Zadanie 4
Dla jakich parametrów \(a,b\in\mathbb{R}\), wektory \(\vec{u}\) i \(\vec{v}\) są prostopadłe:
\(\vec{u}=[a+b,1,b],\,\,\vec{v}=\left[-1,2a,3\right]\)
Zadanie 5
Napisać równanie parametryczne płaszczyzny przechodzącej przez punkty:
\(A=(-1,0,1),\,\,B=(5,0,6),\,\,C=(1,1,1)\)