Znaleźć układ fundamentalny i rozwiązać równanie różniczkowe II-go rzędu o stałych współczynnikach:
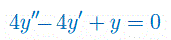
Rozwiązanie widoczne po rejestracji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Znaleźć układ fundamentalny i rozwiązać równanie różniczkowe II-go rzędu o stałych współczynnikach:
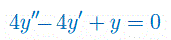
Rozwiązanie widoczne po rejestracji
Komentarzy (3)
Liczymy pierwiastki wielomianu charakterystycznego \(w(\lambda)=4\lambda^2-\lambda+1\).
Liczymy deltę, która wynosi -15, więc pierwiastki są liczbami zespolonymi (tutaj i tutaj możne Pan zobaczyć jak liczy się pierwiastki z liczb ujemnych) \(\lambda_1=\frac{1}{8}-\frac{\sqrt{15}}{8}i\) oraz \(\lambda_2=\frac{1}{8}+\frac{\sqrt{15}}{8}i\)
Rozwiązanie równania różniczkowego 4y''-y'+y=0 jest więc postaci (procedura rozwiązywania opisana jest we wskazówkach do zadania powyżej)
\[y(t)=e^{\frac{t}{8}}\left(C_1\cos \left(\frac{\sqrt{15}}{8}t\right)+C_2\sin \left(\frac{\sqrt{15}}{8}t\right) \right)\]
gdzie \(C_1,C_2\) są stałymi rzeczywistymi. Układ fundamentalny równania różniczkowego 4y''-y'+y=0 stanowią funkcje \[y_1(t)=e^{\frac{t}{8}}\cos \left(\frac{\sqrt{15}}{8}t\right)\]\[y_2(t)=e^{\frac{t}{8}}\sin \left(\frac{\sqrt{15}}{8}t\right)\]Na koniec sprawdzenie wyniku na stronie wolframalpha.com
P.S. 1 Wszystkie zadania rozwiązuję sam, tutaj można znaleźć informacje o mnie ;-)
P.S. 2 Dziękuję za pomoc, postanowiłem przedłużyć ważność Pana abonamentu o jeden dzień.