Rozwiązać równanie różniczkowe z warunkiem początkowym
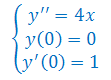
Rozwiązanie

Wskazówki
- Jest to równanie II-go rzędu, które wystarczy scałkować (dwukrotnie), gdyż po lewej stronie równości mamy tylko zmienną y, a po prawej mamy funkcję zależną tylko od x (f(x)=4x)
- Całkujemy równanie po raz drugi i w ten sposób otrzymujemy całkę ogólną równania.
- Podstawiamy wartości z warunków początkowych i obliczamy wartości \(c_1\) i \(c_2\)
Sprawdzenie:
\[y(0)=\frac{2}{3}\cdot 0^3+0=0\]
\[y'(x)=\frac{2}{3}\cdot 3\cdot x^2+1=2x^2+1\]
\[y'(0)=2\cdot 0^2+1=1\]
\[y''(x)=(2x^2+1)'=4x\]

Komentarzy (0)