Rozwiąż równanie różniczkowe korzystając z transformaty Laplace'a:
\(ay'(x)+by(x)+c=0,\,\,a,b,c\in\mathbb{R}\)
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Rozwiąż równanie różniczkowe korzystając z transformaty Laplace'a:
\(ay'(x)+by(x)+c=0,\,\,a,b,c\in\mathbb{R}\)
Znaleźć całkę równania różniczkowego
\(y'=y\)
Rozwiąż równanie różniczkowe
\(y'=1\)
Znaleźć całkę równania różniczkowego
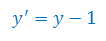
Rozwiązać równanie różniczkowe
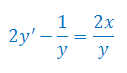
Rozwiązać równanie różniczkowe
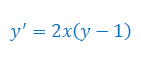
Rozwiązać równanie różniczkowe:
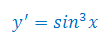
Rozwiązać równanie różniczkowe:
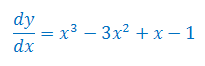
Rozwiązać równanie różniczkowe z warunkiem początkowym:
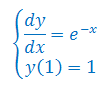
Rozwiązać równanie różniczkowe z warunkiem początkowym:
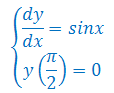
Scałkować podane równanie różniczkowe:
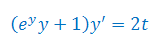
Scałkować podane równanie różniczkowe:
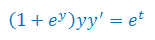
Scałkować podane równanie różniczkowe:
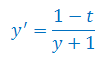
Rozwiązać równanie różniczkowe:
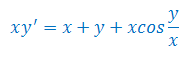
Rozwiązać równanie różniczkowe:
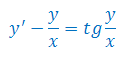
Rozwiązać równanie różniczkowe:
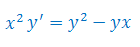
Rozwiązać równanie różniczkowe z warunkiem początkowym:
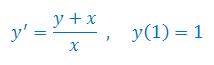
Rozwiązać równanie różniczkowe z warunkiem początkowym:
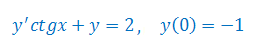
Scałkować podane równanie różniczkowe:
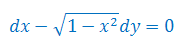
Rozwiązać równanie różniczkowe z warunkiem początkowym:
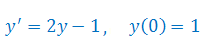
Rozwiązać równanie różniczkowe z warunkiem początkowym
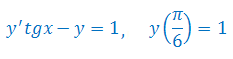
Rozwiązać równanie różniczkowe:
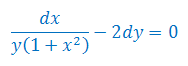
Rozwiązać równanie różniczkowe:
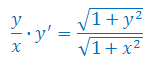
Rozwiązać równanie różniczkowe:
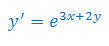
Rozwiązać równanie różniczkowe:
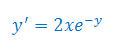
Rozwiązać równanie różniczkowe:
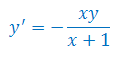
Rozwiązać równanie różniczkowe:
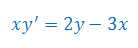
Znaleźć całkę równania różniczkowego
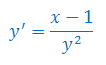
Rozwiązać równanie różniczkowe
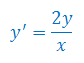
Rozwiązać równanie różniczkowe
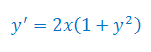
Rozwiąż równanie różniczkowe pierwszego rzędu
\(y'=\frac{1}{x^2+1}\)
Rozwiązać równanie różniczkowe II-go rzędu:
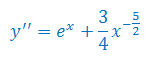
Rozwiązać równanie różniczkowe z warunkiem początkowym:
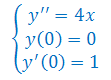
Znaleźć układ fundamentalny i rozwiązać równanie różniczkowe II-go rzędu o stałych współczynnikach:
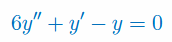
Znaleźć układ fundamentalny i rozwiązać równanie różniczkowe II-go rzędu o stałych współczynnikach:
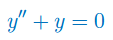
Znaleźć układ fundamentalny i rozwiązać równanie różniczkowe II-go rzędu o stałych współczynnikach:
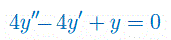
Rozwiązać równanie różniczkowe z warunkiem początkowym:
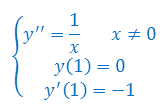
Rozwiązać równanie różniczkowe II-go rzędu:
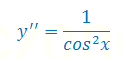
Znaleźć rozwiązanie równania różniczkowego spełniające warunek początkowy przy użyciu wielomianu charakterystycznego oraz za pomocą transformaty Laplace'a:
\(x''-x=0,\,\,x(0)=1,\,x'(0)=0\)
Znaleźć rozwiązanie równania różniczkowego niejednorodnego spełniające warunek początkowy przy użyciu wielomianu charakterystycznego oraz za pomocą transformaty Laplace'a:
\(x''-x=e^{-t},\,\,x(0)=1,\,x'(0)=0\)
Rozwiąż równanie różniczkowe niejednorodne przy użyciu wielomianu charakterystycznego oraz za pomocą transformaty Laplace'a:
\(y''+9y=e^{x}\cos(3x)\)
Podaj szkic schematu rozwiązywania równania różniczkowego II-go rzędu niejednorodnego za pomocą transformaty Laplace'a:
\(a y''(x)+by'(x)+cy(x)=f(x),\,\,a,b,c\in\mathbb{R}\)
Podaj szkic schematu rozwiązywania równania różniczkowego II-go rzędu niejednorodnego za pomocą wielomianu charakterystycznego:
\(a y''(x)+by'(x)+cy(x)=f(x),\,\,a,b,c\in\mathbb{R}\)
Rozwiąż równanie różniczkowe drugiego rzędu
\(y''=\frac{1}{x^2+1}\)
Jesteś w kategorii Równania różniczkowe zadania z rozwiązaniami
W tej kategorii znajdziesz rozwiązania typowych zadań dotyczących równań różniczkowych zwyczajnych (czyli dotyczących funkcji jednej zmiennej), w tym przykłady z równań różniczkowych I-go i II-go rzędu, zagadnienia Cauchy'ego (zagadnienia początkowe lub z warunkami początkowymi). Równania różniczkowe opisują wiele zjawisk rzeczywistych (związanych np. ze zmianą zjawiska w czasie, przestrzeni itp.), dlatego są bardzo użyteczne w różnych zagadnieniach techniki i przemysłu, a także np. w fizyce i finansach.
Typowe schematy rozwiązywania równań różniczkowych zwyczajnych zależą od ich postaci. Mamy np. równania różniczkowe I-go rzędu o rozdzielonych zmiennych, równania jednorodne, liniowe itd. Do rozwiązywania równań różniczkowych liniowych można użyć metody uzmienniania stałej lub przewidywania (postaci rozwiązania). W przypadku równań różniczkowych liniowych rzędu II-go podstawowym narzędziem jest tzw. układ fundamentalny, do którego wyznaczenia stosujemy wyznacznik Wrońskiego (wrońskian). W przypadku równań różniczkowych liniowych II-go rzędu o stałych wzpółczynnikach podstawowym narzędziem jest równanie charakterystyczne, które pozwala określić postać całek szczególnych i całki ogólnej.
Po zapoznaniu się z możliwie dużą liczbą rozwiązań zadań z równań różniczkowych, warto próbować samodzielnie rozwiązać ponownie te same zadania, ale zaglądać do rozwiązań zamieszczonych na stronie jedynie w ramach podpowiedzi lub w celu sprawdzenia wyniku. Warto pamiętać, że pod każdym zadaniem istnieje możliwość zadania pytania w komentarzu. Zwróć uwagę, że tylko pełne zrozumienie rozwiązania zadania (oraz schematów i pojęć, które zostały w nim użyte) pozwala później na samodzielne rozwiązanie podobnego zadania w czasie trwania kolokwium lub egzaminu. Zadania z równań różniczkowych nie należą do łatwych, dlatego opanowanie wszystkich schematów i metod rozwiązywania równań różniczkowych zajmuje sporo czasu i wymaga wiele pracy.