Stosując rozwinięcie Laplace'a oblicz wyznacznik macierzy 4x4
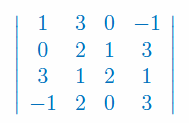
Rozwiązanie
Stosujemy rozwinięcie Laplace'a względem 3 kolumny (wybieramy właśnie tą kolumnę, ponieważ posiada ona aż dwa zera - dzięki temu będzie się szybciej i łatwiej liczyło):

Obliczenia pomocnicze - dwa ostatnie wyznaczniki stopnia 3 (stosujemy rozwinięcia Laplace'a względem 1 kolumny):
\[\begin{vmatrix}\color{red}1&3&-1\\\color{red}3&1&1\\\color{red}{-1}&2&3\end{vmatrix}=\color{red}{1}\cdot (-1)^{1+1}\begin{vmatrix}1&1\\2&3\end{vmatrix}+\color{red}{3}\cdot (-1)^{2+1}\begin{vmatrix}3&-1\\2&3\end{vmatrix}+(\color{red}{-1})\cdot (-1)^{3+1}\begin{vmatrix}3&-1\\1&1\end{vmatrix}=\]\[=1\cdot1\cdot (1\cdot 3-2\cdot 1)+3\cdot (-1)\cdot (3\cdot 3-2\cdot (-1))+(-1)\cdot 1\cdot (3\cdot 1-1\cdot (-1))=1-33-4=-36\]
\[\begin{vmatrix}\color{red}1&3&-1\\\color{red}0&2&3\\\color{red}{-1}&2&3\end{vmatrix}=\color{red}{1}\cdot (-1)^{1+1}\begin{vmatrix}2&3\\2&3\end{vmatrix}+\color{red}{0}\cdot (-1)^{2+1}\begin{vmatrix}3&-1\\2&3\end{vmatrix}+(\color{red}{-1})\cdot (-1)^{3+1}\begin{vmatrix}3&-1\\2&3\end{vmatrix}=\]\[=1\cdot1\cdot (2\cdot 3-2\cdot 3)+0+(-1)\cdot 1\cdot (3\cdot 3-2\cdot (-1))=0+0-11=-11\]
Wskazówki:
- Przy stosowaniu rozwinięcia Laplace'a do liczenia wyznacznika macierzy wybieramy zawsze wiersz lub kolumnę, która posiada najwięcej zer - pozwala to znacznie uprościć i przyspieszyć obliczenia.
Aby to dobrze zrozumieć, spróbuj obliczyć wyznacznik macierzy 4x4 lub 5x5 stosując rozwinięcie względem wiersza lub kolumny, która nie ma żadnych zer... - Do liczenia wyznaczników macierzy stopnia 3 można używać rozwinięcia Laplace'a lub metody Sarrusa (zobacz przykłady tutaj).
Przy obliczeniach pomocniczych użyliśmy rozwinięć Laplace'a względem 1 kolumny. - Wyznacznik macierzy stopnia 2 liczymy ze wzoru:
\(\left|\begin{array}{cc}a&b\\c&d\end{array}\right|=a\cdot d-b\cdot c\)
Schemat rozwinięcia Laplace'a
W przypadku macierzy A stopnia n, schemat metody Laplace'a wygląda następująco:
1. Wybieramy wiersz lub kolumnę macierzy, w której znajduje się najwięcej zer
2. "Rozwijamy" wyznacznik względem wybranego wiersza lub kolumny wyliczając wyznaczniki macierzy stopni n-1 (dopełnienia algebraiczne kolejnych elementów).
W przypadku rozwinięcia względem i-tego wiersza (gdzie \(i=1,2,\ldots,n\)) schemat metody Laplace'a wygląda następująco:
\[\det A=a_{i1}\cdot (-1)^{i+1}\cdot\det A_{i1}+a_{i2}\cdot (-1)^{i+2}\cdot\det A_{i2}+\ldots +a_{in}\cdot (-1)^{i+j} \cdot\det A_{in}=\]\[=\sum\limits_{k=1}^n a_{ik}\cdot (-1)^{i+k}\cdot \det A_{ik}\]
gdzie \(A_{ij}\) jest macierzą stopnia n-1 otrzymaną z macierzy A przez skreślenie i-tego wiersza i j-tej kolumny (\(\det A_{ij}\) to minor macierzy), np. \(A_{12}\) to macierz powstała przez usunięcie 1-go wiersza i 2-giej kolumny w macierzy A.
Zauważ, że \((-1)^{i+k}\) będzie na przemian równe -1 i 1 lub 1 i -1, więc w rozwinięciu Laplace'a kolejne wyrażenia mają na przemian znak minus i plus (lub plus i minus).
W przypadku rozwinięcia względem j-tej kolumny (gdzie \(j=1,2,\ldots,n\)) mamy następujący wzór na wyznacznik:
\[\det A=a_{1j}\cdot (-1)^{1+j}\cdot \det A_{1j}+a_{2j}\cdot (-1)^{2+j}\cdot \det A_{2j}+\ldots +a_{nj}\cdot (-1)^{n+j}\cdot\det A_{nj}=\]\[=\sum\limits_{k=1}^n a_{kj}\cdot (-1)^{k+j}\cdot\det A_{kj}\]
np. gdy \(j=1\) to rozwinięcie Laplace'a następuje względem pierwszej kolumny:
\[\det A=a_{11}\cdot (-1)^{1+1}\cdot\det A_{11}+a_{21}\cdot (-1)^{2+1}\cdot\det A_{21}+\ldots +a_{n1}\cdot (-1)^{n+1}\cdot\det A_{n1}=\]\[=a_{11}\cdot\det A_{11}-a_{21}\cdot\det A_{21}+\ldots +a_{n1}\cdot (-1)^{n+1}\cdot\det A_{n1}\]
Używając dopełnień algebraicznych rozwinięcie Laplace'a względem i-tego wiersza można zapisać następująco:
\[\det A=a_{i1}\cdot D_{i1}+a_{i2}\cdot D_{i2}+\ldots +a_{in}\cdot D_{in}=\sum\limits_{k=1}^n a_{ik}\cdot D_{ik}\]
Natomiast rozwinięcie względem j-tej kolumny wygląda tak:
\[\det A=a_{1j}\cdot D_{1j}+a_{2j}\cdot D_{2j}+\ldots +a_{nj}\cdot D_{nj}=\sum\limits_{k=1}^n a_{kj}\cdot D_{kj}\]

Komentarzy (7)
Mogę polecić następujące pozycje:
Algebra liniowa 1. Przykłady i zadania, Zbigniew Skoczylas
Algebra liniowa w zadaniach, Jerzy Rutkowski
Kupię natychmiast
Andrzej
Przy stosowaniu metody Laplace'a generalnie w kolejnych składniach (przy kolejnych wyznacznikach) mamy na przemian znak + i - (wynika to z występowania -1 na przemian do potęg parzystych i nieparzystych).