Oblicz wyznacznik macierzy stopnia 3
\[\begin{vmatrix}5&-1&3\\0&1&-2\\4&3&2\end{vmatrix}\]
Rozwiązanie
Stosujemy metodę Sarrusa:
\[\begin{vmatrix}5&-1&3\\0&1&-2\\4&3&2\end{vmatrix}\begin{matrix}5&-1\\0&1\\4&3\end{matrix}=5\cdot 1\cdot 2+(-1)\cdot (-2)\cdot 4+3\cdot 0\cdot 3+\]\[-3\cdot 1\cdot 4-5\cdot (-2)\cdot 3-(-1)\cdot 0\cdot 2=10+8+0-12+30-0=36\]
UWAGA: Metodę Sarrusa można stosować tylko i wyłącznie do obliczania wyznaczników stopnia 3. Do obliczania wyznaczników dowolnych stopni (także stopnia 3) można użyć operacji elementarnych i rozwinięcia Laplace'a
Wskazówki
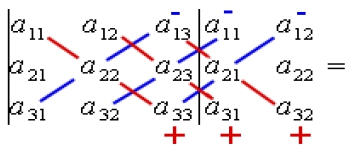
Schemat metody Sarrusa:
![]()
Reguła Sarrusa polega na dopisaniu po prawej stronie obok wyznacznika dwóch pierwszych kolumn macierzy i następnie wymnożenie elementów wzdłuż ukośnych linii tak jak widać na schemacie powyżej.
Uwaga: Metoda Sarrusa nie jest jakąś "magiczną" metodą liczenia wyznacznika macierzy stopnia 3. Wynik otrzymany tą metodą jest oczywiście identyczny jak po zastosowaniu rozwinięcia Laplace'a.

Komentarzy (8)
Jest to zapis jaki się stosuje przy zapisywaniu jednego wyrażenia matematycznego w kilku linijkach. Gdy jest minus, to linię kończy się plusem, a minus pisze się w następnej linii na samym początku. Pozwala to uniknąć nieporozumień.
Czy na końcu wiersza "5⋅1⋅2+(−1)⋅(−2)⋅4+3⋅0⋅3+" nie powinno być - (minus) na końcu?