Rozwiąż równanie zespolone wiedząc, że \(Im(z)=1\):
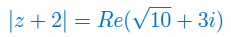
Rozwiązanie widoczne po rejestracji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Komentarzy (2)
pozrawiam
janiszewski