Korzystając ze wzoru de Moivre'a oblicz potęgę:
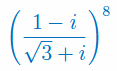
Rozwiązanie widoczne po rejestracji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Korzystając ze wzoru de Moivre'a oblicz potęgę:
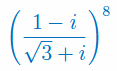
Rozwiązanie widoczne po rejestracji
Komentarzy (6)
Z góry dziękuję za odp ;)
(przy cosinusie pojawi się minus, a przy sinusie zostaje znak plus):
\[\cos\left(\frac{2}{3}\pi\right)=\cos\left(\pi-\frac{1}{3}\pi\right)=-\cos\left(\frac{1}{3}\pi\right)=-\cos\left(\frac{\pi}{3}\right)\\ \sin\left(\frac{2}{3}\pi\right)=\sin\left(\pi-\frac{1}{3}\pi\right)=\sin\left(\frac{1}{3}\pi\right)=\sin\left(\frac{\pi}{3}\right)\]
Wzorów redukcyjnych warto nauczyć się na pamięć (proszę zerknąć tutaj), ale można też pomagać sobie wykresami funkcji trygonometrycznych. Proszę pytać śmiało jeśli będą jeszcze jakieś problemy.
Jak przeszliśmy z cos 2/3 pi + isin 2/3 pi na -cos pi/3 + isin pi/3 ?
Z góry dziękuję za odpowiedź!