Określ dziedzinę funkcji (dla \(x\in\mathbb{R}\))
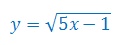
Rozwiązanie
Sprawdzamy dla jakich "x" wyrażenie pod pierwiastkiem jest nieujemne:
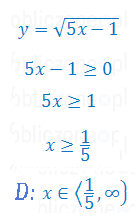
Na koniec wykres funkcji \(y=\sqrt{5x-1}\), na którym widać,
że funkcja nie przyjmuje żadnych wartości dla \(x<\frac{1}{5}\):
UWAGA: Najedź myszką na wykres i przytrzymaj lewy przycisk, aby dowolnie przesuwać i powiększyć funkcję.
Wskazówki
W przykładzie sprawdzamy dla jakich x, wyrażenie stojące pod pierwiastkiem jest większe bądź równe zero (ponieważ pierwiastek z liczby ujemnej nie istnieje, chyba, że dopuścimy liczby zespolone ;-)).
Dziedzina funkcji - co to jest?
Dziedzina funkcji jest to zbiór takich x, dla których istnieją wartości funkcji (czyli są to wszystkie x, które można podstawić do wzoru funkcji).
Innymi słowy dziedzina jest zbiorem wszystkich argumentów funkcji.
Wyznaczanie dziedziny funkcji - przydatne wskazówki
W zadaniach zwracaj zawsze uwagę na działania niedozwolone w matematyce. Pomogą Ci one wyznaczyć warunki dla \(x\) należących do dziedziny. Niedozwolone jest:
- pierwiastkowanie (stopnia parzystego) liczb ujemnych, np. gdy\[f(x)=\sqrt{g(x)},\,\,\textrm{to}\,\,g(x)\ge 0\]
- dzielenie przez 0, np. gdy\[f(x)=\frac{g(x)}{h(x)},\,\,\textrm{to}\,\,h(x)\neq 0\]
- logarytmowanie liczb ujemnych, np. gdy\[f(x)=\log(g(x)),\,\,\textrm{to}\,\,g(x)>0\]

Komentarzy (2)