Oblicz granicę ciągu:
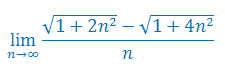
Rozwiązanie widoczne po rejestracji
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Oblicz granicę ciągu:
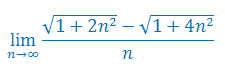
Rozwiązanie widoczne po rejestracji
Komentarzy (6)
\[\frac{\sqrt{1+2n^2}-\sqrt{1+4n^2}}{n}\cdot \frac{\sqrt{1+2n^2}+\sqrt{1+4n^2}}{\sqrt{1+2n^2}+\sqrt{1+4n^2}}=\frac{1+2n^2-(1+4n^2)}{n\cdot (\sqrt{1+2n^2}+\sqrt{1+4n^2})}=\]\[=\frac{1+2n^2-1-4n^2}{n\cdot (\sqrt{1+2n^2}+\sqrt{1+4n^2})}=\frac{-2n^2}{n\cdot (\sqrt{1+2n^2}+\sqrt{1+4n^2})}=\frac{-2n}{\sqrt{1+2n^2}+\sqrt{1+4n^2}}=\]\[=\frac{-2n}{n\sqrt{\frac{1}{n^2}+2}+n\sqrt{\frac{1}{n^2}+4}}=\frac{-2}{\sqrt{\frac{1}{n^2}+2}+\sqrt{\frac{1}{n^2}+4}}\rightarrow \frac{-2}{\sqrt{2}+2}=\sqrt{2}-2\]
Jak widać dochodzimy do równie skomplikowanego wyrażenia jak to początkowe, ale da się i w ten sposób dojść do wyniku :-)