Zbadaj zbieżność szeregu liczbowego:
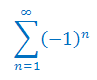
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Zbadaj zbieżność szeregu liczbowego:
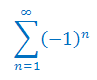
Wykaż, że dla \(|q|<1\) zbieżny jest szereg geometryczny:
\(\sum\limits_{n=0}^\infty q^n=1+q+q^2+q^3\,+\,...\)
Znaleźć sumy częściowe szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \left(\frac{1}{n}-\frac{1}{n+1}\right)\)
Wykaż, że szereg liczbowy jest rozbieżny:
\(\sum\limits_{n=1}^\infty n=1+2+3\,+\,...\)
Korzystając z kryterium porównawczego zbadać zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{|\sin(n!)|}{2^n}\)
Korzystając z kryterium ilorazowego zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{3n+1}{n^4+n+2}\)
Korzystając z kryterium Cauchy'ego zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{n}{2^n}\)
Korzystając z kryterium d'Alemberta zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{n!}{n^n}\)
Korzystając z kryterium całkowego zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{1}{n}\)
Korzystając z kryterium Leibniza zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{(-1)^n}{n}\)
Zbadaj zbieżność szeregu liczbowego korzystając z kryterium Cauchy'ego:
\(\sum\limits_{n=0}^\infty \left(1+\frac{1}{5^n}\right)^{n5^n}\)
Korzystając z kryterium Cauchy'ego zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{(n!)^n}{n^{n^2}}\)
Zbadaj zbieżność szeregu liczbowego korzystając z kryterium Cauchy'ego:
\(\sum\limits_{n=1}^\infty \left(\frac{n+1}{n}\right)^{n^2}\)
Zbadaj zbieżność szeregu liczbowego korzystając z kryterium Cauchy'ego:
\(\sum\limits_{n=1}^\infty \left(\frac{n-1}{n}\right)^{n^2}\)
Korzystając z kryterium Cauchy'ego zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{\left(\frac{n+1}{n}\right)^{n^2}}{2^{n}}\)
Zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{n^n}{2^{n^2}}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{2}{n!}\)
Korzystając z kryterium d'Alemberta zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty \frac{e^{4n-1}}{n3^n}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty\sqrt[n]{\frac{1}{n}}\)
Korzystając z warunku koniecznego zbieżności szeregów liczbowych wykaż, że szereg jest rozbieżny:
\(\sum\limits_{n=1}^\infty{\frac{n+2}{n+100}}\)
Korzystając z warunku koniecznego zbieżności szeregów liczbowych pokaż, że szereg jest rozbieżny:
\(\sum\limits_{n=1}^\infty\left(\frac{n+1}{n}\right)^n\)
Korzystając z kryterium Leibniza zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty (-1)^n\frac{1}{2n+1}\)
Korzystając z kryterium Leibniza zbadaj zbieżność szeregu:
\(\sum\limits_{n=1}^\infty (-1)^n\frac{1}{\sqrt{2n+1}}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{n!3^n}{n^n}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{n!2^n}{n^n}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{(n!)^2}{(2n)!}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=2}^\infty \frac{1}{n\ln n}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{4^n}{n!}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{1}{n^n}\)
Zbadaj zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{n^4}{4^n}\)
Zbadać zbieżność szeregu liczbowego:
\(\sum\limits_{n=1}^\infty \frac{\ln(n)}{n}\)
Zbadaj zbieżność szeregu w zależności od parametru p:
\(\sum\limits_{n=1}^\infty \frac{1}{n^p}\)
Zbadaj zbieżność szeregu liczbowego:
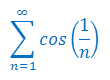
Zbadaj zbieżność szeregu liczbowego:
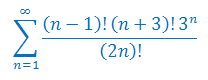
Zbadaj zbieżność szeregu liczbowego:
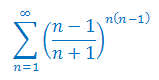
Zbadaj zbieżność szeregu liczbowego:
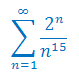
Jesteś w kategorii Szeregi liczbowe zadania z rozwiązaniami
Szereg liczbowy to nieskończona suma wyrazów ciągu liczbowego. Czy łatwo obliczyć sumę szeregu liczbowego? Bardzo trudno (no może poza sumą szeregu geometrycznego), ale za to można sprawdzić, czy dany szereg jest zbieżny czy rozbieżny, tzn. czy jego suma jest skończona czy nieskończona. Do sprawdzania zbieżności szeregów liczbowych wykorzystuje się kryteria zbieżności, takie jak kryterium porównacze, Cauchy'ego, de Alemberta, całkowe, ilorazowe czy Dirichleta.