Podaj wzór na granicę ciągu:
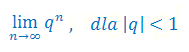
NAUCZ SIĘ JEDNEGO DZIAŁU MATEMATYKI WYŻSZEJ W 3 DNI
Wystarczy uczyć się na przykładach, a teorię OGARNĄĆ przy okazji
Na pokładzie mamy już 30 000 studentów. Dołącz i Ty!
Podaj wzór na granicę ciągu:
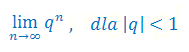
Oblicz granicę ciągu liczbowego:
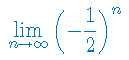
Oblicz granicę ciągu:
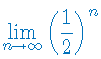
Obliczyć granicę ciągu liczbowego:
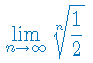
Oblicz granicę ciągu:
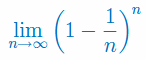
Podaj wzór na granicę:
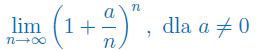
Obliczyć granicę ciągu liczbowego:
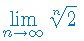
Oblicz granicę ciągu:
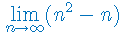
Oblicz granicę ciągu liczbowego:
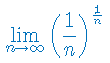
Wykaż, że granica ciągu nie istnieje:
\(\lim\limits_{n\to +\infty} (-1)^n\)
Oblicz granicę ciągu:
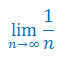
Podaj wzór na granicę:
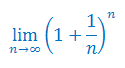
Podaj wzór na granicę ciągu liczbowego:
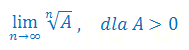
Oblicz granicę ciągu liczbowego:
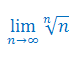
Oblicz granicę ciągu o wyrazie ogólnym \(a_n\), jeśli
\(a_n=\sqrt{2n}-\sqrt{n+10}\)
Oblicz granicę:
\(\lim\limits_{n\to\infty} \frac{a_{n+1}}{a_n},\,\,\,\textrm{gdzie}\,\,a_n=\frac{n!}{n^n}\)
Wykaż, że dla \(a>0,\,\,b>0,\,c>0\) granica ciągu wynosi:
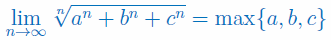
Wykaż, że dla \(a>0,\,\,b>0\) granica ciągu wynosi:
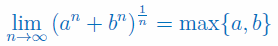
Oblicz granicę ciągu:
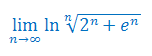
Oblicz granicę ciągu:
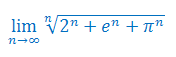
Oblicz granicę ciągu korzystając z twierdzenia o trzech ciągach:
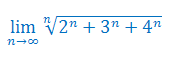
Oblicz granicę ciągu:
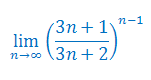
Oblicz granicę ciągu:
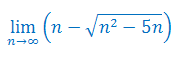
Oblicz granicę ciągu:
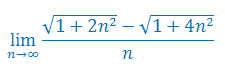
Oblicz granicę ciągu:
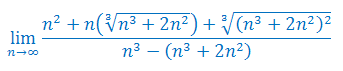
Oblicz granicę ciągu:
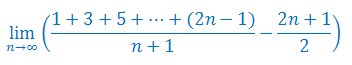
Oblicz granicę ciągu:
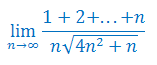
Oblicz granicę ciągu:
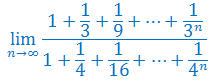
Oblicz granicę ciągu:
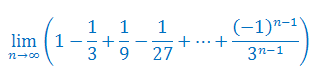
Oblicz granicę ciągu:
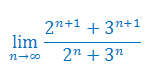
Oblicz granicę ciągu:
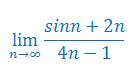
Oblicz granicę ciągu:
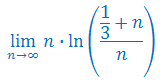
Oblicz granicę ciągu:
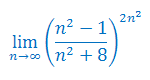
Oblicz granicę ciągu:
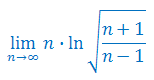
Oblicz granicę ciągu:
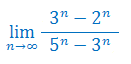
Oblicz granicę ciągu:
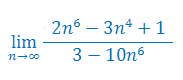
Oblicz granicę ciągu:
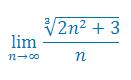
Oblicz granicę ciągu:
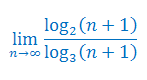
Jesteś w kategorii Granice ciągów zadania z rozwiązaniami
W tym dziale znajdziesz przykłady jak obliczać granice ciągów oraz poznasz podstawowe wzory na granice typu \(q^n,\,\,\sqrt[n]{n},\,\,\sqrt[n]{A}\) oraz na ganice, których wynikiem jest liczba e. Nauczysz się również jak stosować twierdzenie o dwóch i trzech ciągach oraz co należy wyciągnąć przed nawias ze złożonego wyrażenie, aby móc obliczyć granicę (szczególnie w przypadku ilorazów i ciągów liczbowych zawierających pierwiastki). Nie zapomnij o przykładach liczenia granic z sum n wyrazowych, do których liczenia należy wykorzystać wzór na sumę ciągu arytmetycznego lub geometrycznego.