Oblicz całkę oznaczoną
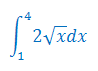
Rozwiązanie
Obliczenie całki oznaczonej sprowadza się tak naprawdę do obliczenia całki nieoznaczonej i następnie wyliczenie wartości otrzymanej funkcji w granicach całkowania:
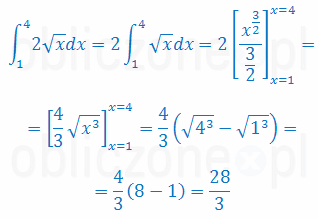
Wskazówki
- Korzystamy z podstawowego wzoru na całkę nieoznaczoną funkcji elementarnej:
\(\int x^n\,dx=\frac{x^{n+1}}{n+1}+c\) - Pamiętamy o obliczeniu różnicy wartości funkcji w punktach równych 1 i 4, zgodnie z definicją całki oznaczonej
\(\int_a^b f(x)\,dx=F(b)-F(a)\)
gdzie F(x) jest funkcją pierwotną funkcji f(x), czyli
\(F(x)=\int f(x)\,dx\)

Komentarzy (0)